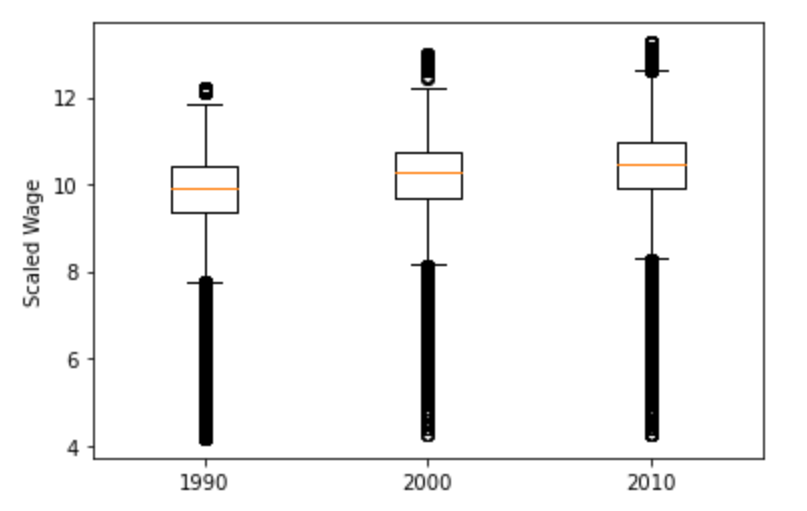
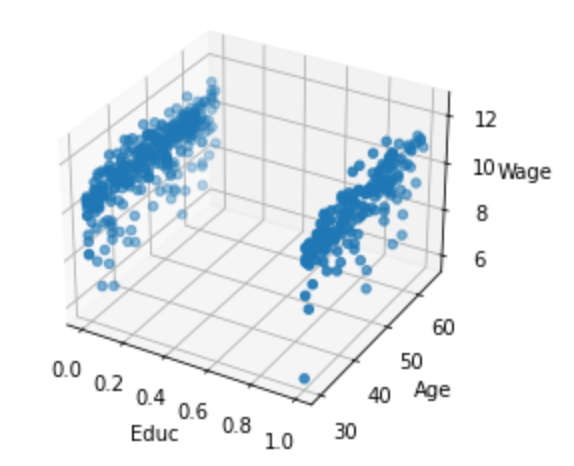
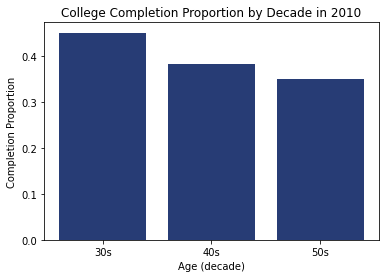
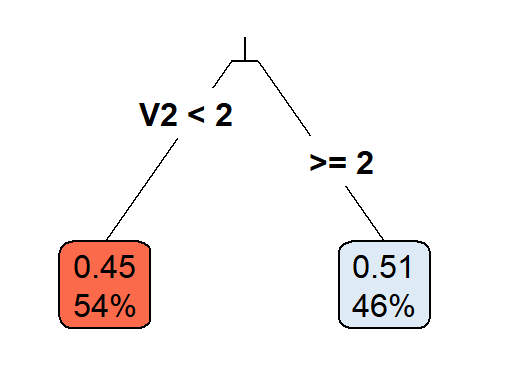
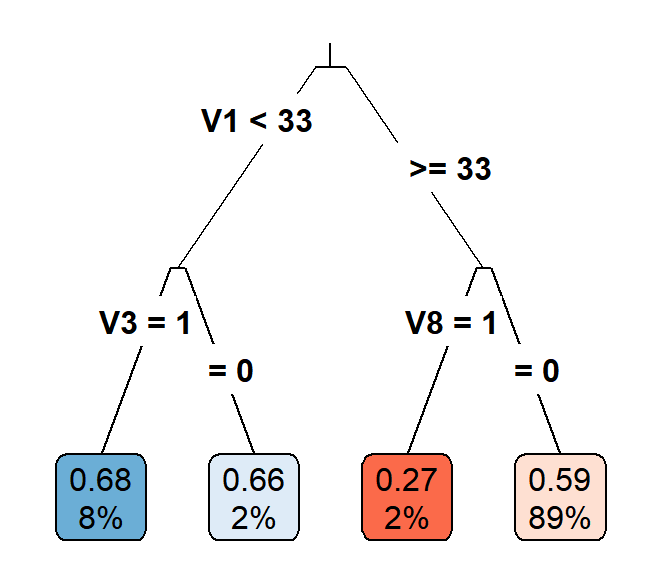
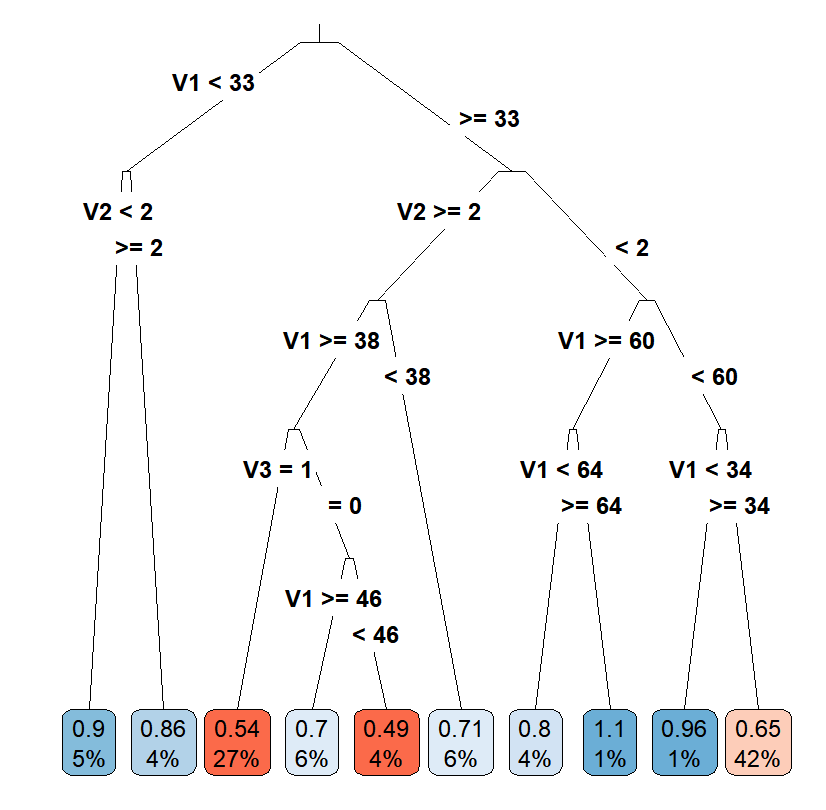
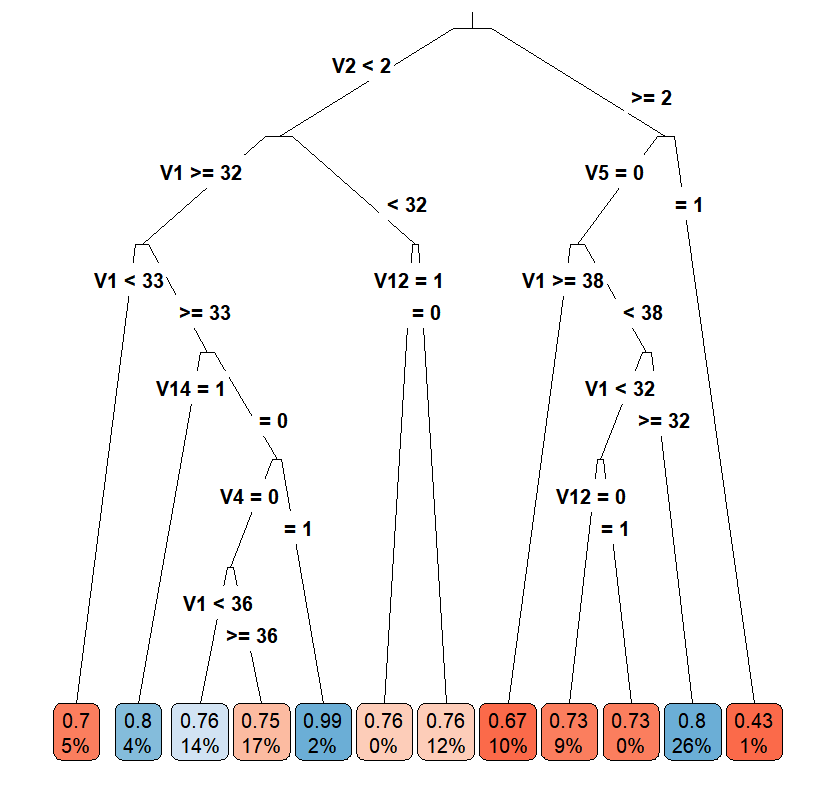
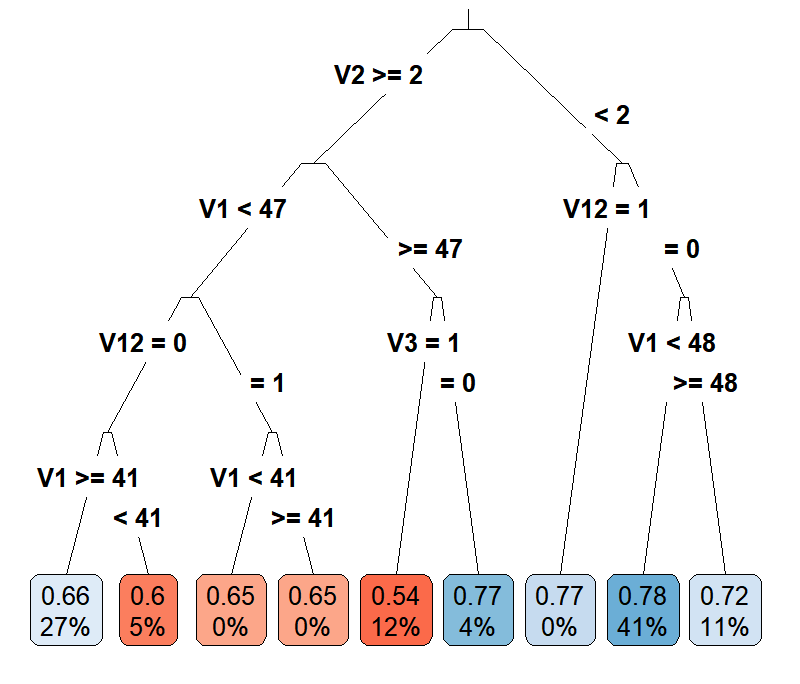
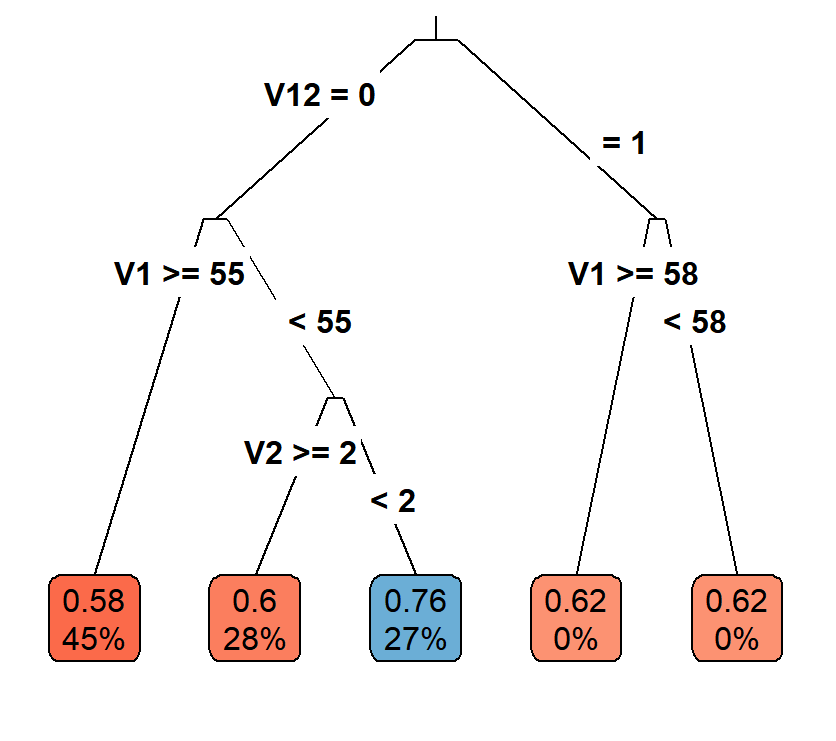
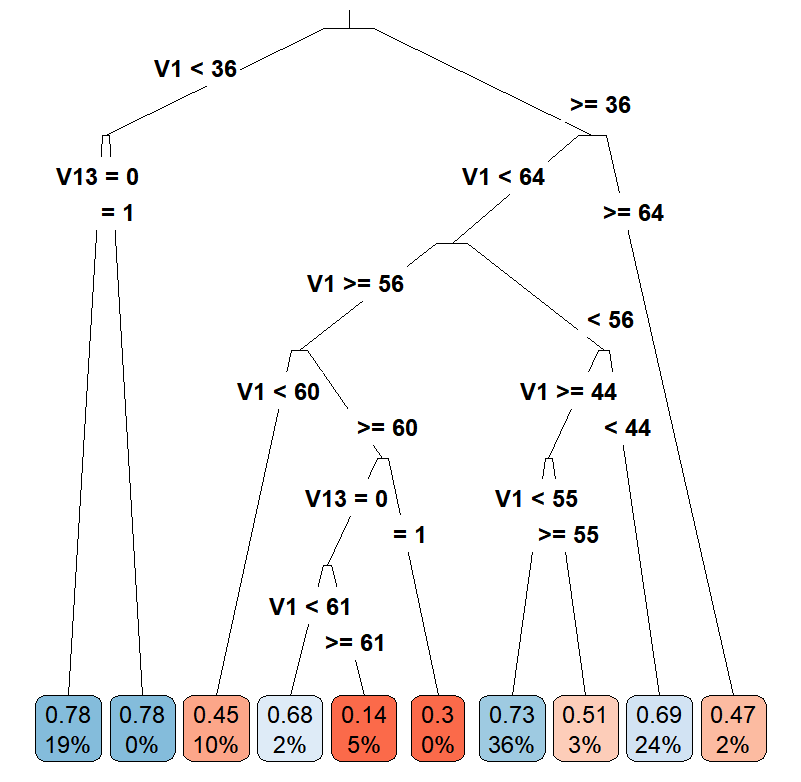
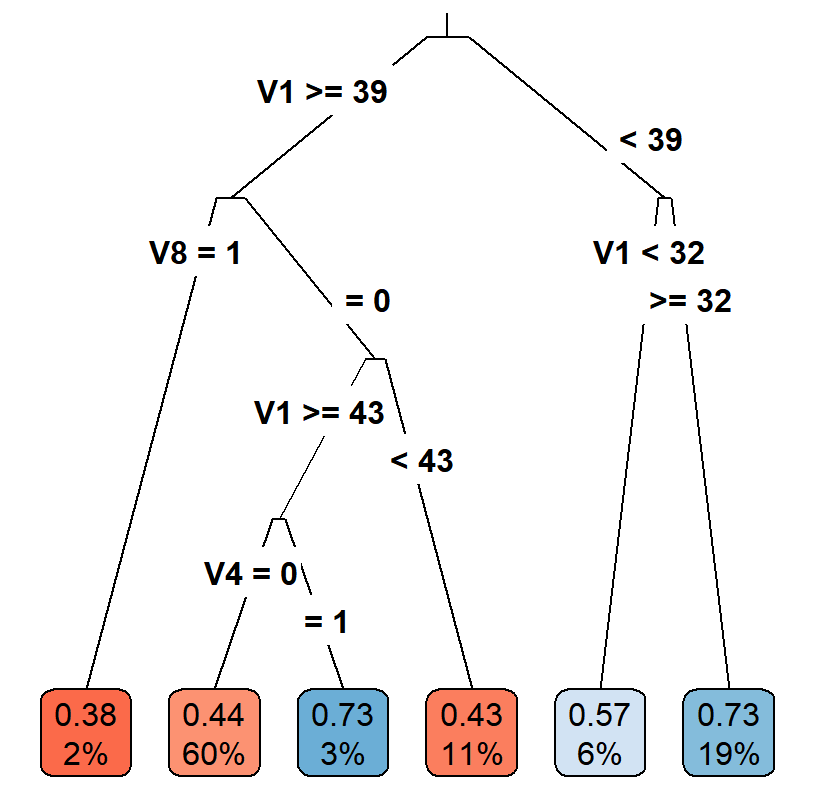
Casual Tree & CATE Estimation
The "honest" approach used for building and validating the Causal Tree is an extension and divergence from the classification and regression trees(CART) algorithm. One of the most important concerns is to find criteria to evaluate and compare estimators for treatment effects. Due to the fact that we cannot observe both \(Y_i(1)\) and \(Y_i(0)\) for an individual, the true treatment effect \(\tau\) is also not observable since we are missing half of the \(Y^{obs}\). Thus, the "honest" version of \(EMSE_{\tau}(\Pi)\): \[EMSE_{\tau}(\Pi)\equiv\mathbb{E}_{S^{te},S^{est}}[MSE_{\tau}(S^{te},S^{est},\Pi)]\] is not feasible as we have no knowledge about \(\tau_i\). Therefore, the paper proposed an estimator for \(EMSE_{\tau}(\Pi)\) by modifying the \(MSE_{\mu}\) in CART to get an unbiased estimator \(\widehat{MSE}_{\tau}\) for the treatment effect and the \(EMSE_{\tau}(\Pi)\) in "honest" algorithm to get an unbiased estimator \(\widehat{EMSE}_{\tau}(S^{tr},N^{est},\Pi)\) for \(EMSE_{\tau}(\Pi)\). Let \(p\) denote the proportion of the treated individuals in a leaf, \(S_{control}^{tr}\) denote the subsample of the control group in the training sample, and \(S_{treat}^{tr}\)$ denote the subsample of the treatment group in the training sample, the unbiased estimator for \(EMSE_{\tau}(\Pi)\) for splitting is defined as \[-\widehat{EMSE}_{\tau}(S^{tr},N^{est},\Pi)\equiv\frac{1}{N^{tr}}\sum_{i \in S^{tr}}\hat{\tau}^2(X_i;S^{tr},\Pi)-(\frac{1}{N^{tr}}+\frac{1}{N^{est}})\cdot \sum_{l \in \Pi}(\frac{S_{S_{treat}^{tr}}^2(l)}{p}+\frac{S_{S_{control}^{tr}}^2(l)}{1-p}).\] Using the same equation as the splitting criterion with cross-validation sample, the unbiased estimator of \(EMSE_{\tau}(\Pi)\) for cross-validation is \(-\widehat{EMSE}_{\tau}(S^{tr,cv},N^{est},\Pi)\).